VECTORS.
This is a vector:
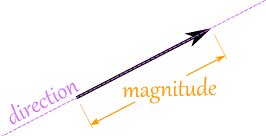
The length of the line shows its magnitude and the arrowhead points in the direction.
You can add two vectors by simply joining them head-to-tail:
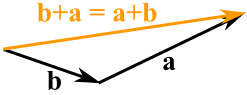
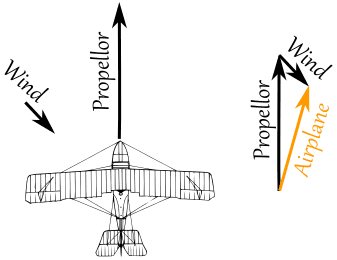
Example: A plane is flying along, pointing North, but there is a wind coming from the North-West.
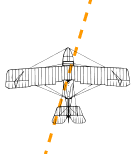
If you watched the plane from the ground it would seem to be slipping sideways a little.
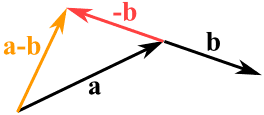
Subtracting
You can also subtract one vector from another:- first you reverse the direction of the vector you want to subtract,
- then add them as usual:
Other Notation
| A vector can also be written as the letters of its head and tail with an arrow above, like this: |
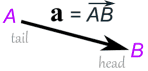 |
Calculations
Now ... how do we do the calculations?The most common way is to break up a vector into x and y pieces, like this:
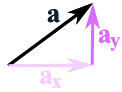
The vector a is broken up into
the two vectors ax and ay
the two vectors ax and ay
Adding Vectors
And here is how to add two vectors after breaking them into x and y parts: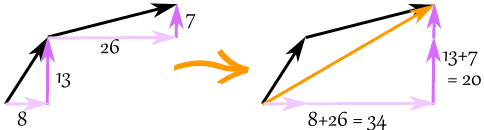
The vector (8,13) and the vector (26,7) add up to the vector (34,20)
Example: add the vectors a = (8,13) and b = (26,7)
c = a + b
c = (8,13) + (26,7) = (8+26,13+7) = (34,20)
c = a + b
c = (8,13) + (26,7) = (8+26,13+7) = (34,20)
Subtracting Vectors
Remember: to subtract, first reverse the vector you want to subtract, then add.
Example: subtract k = (4,5) from v = (12,2)
a = v + −k
a = (12,2) + −(4,5) = (12,2) + (−4,−5) = (12−4,2−5) = (8,−3)
a = v + −k
a = (12,2) + −(4,5) = (12,2) + (−4,−5) = (12−4,2−5) = (8,−3)
Magnitude of a Vector
The magnitude of a vector is shown by two vertical bars on either side of the vector:
|a|
OR it can be written with double vertical bars (so as not to confuse it with absolute value):
||a||
You can use Pythagoras' theorem to calculate it:
|a| = √( x2 + y2 )
Example: what is the magnitude of the vector b = (6,8) ?
|b| = √( 62 + 82 ) = √( 36+64 ) = √100 = 10
A vector with magnitude 1 is called a Unit Vector. |b| = √( 62 + 82 ) = √( 36+64 ) = √100 = 10
Vector vs Scalar
When using vectors we call an ordinary number a "scalar".
Scalar: just a number (like 7 or −0.32) ... definitely not a vector.
A vector is often written in bold,
so c is a vector, it has magnitude and direction
but c is just a value, like 3 or 12.4
but c is just a value, like 3 or 12.4
Example: kb is actually the scalar k times the vector b.
Multiplying a Vector by a Scalar
When you multiply a vector by a scalar it is called "scaling" a vector, because you change how big or small the vector is.
Example: multiply the vector m = (7,3) by the scalar 3
It still points in the same direction, but is 3 times longer
(And now you know why numbers are called "scalars", because they "scale" the vector up or down.)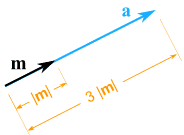 |
a = 3m = (3×7,3×3) = (21,9) |
Multiplying a Vector by a Vector (Dot Product and Cross Product)
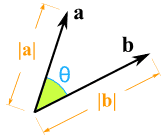 |
How do you multiply two vectors together? There is more than one way!
|
More Than 2 Dimensions
The vectors we have been looking at have been 2 dimensional, but vectors work perfectly well in 3 or more dimensions: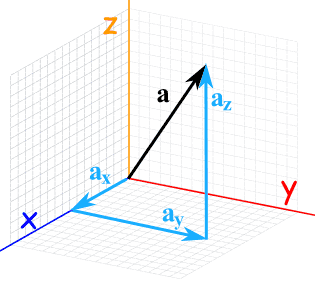
Example: add the vectors a = (3,7,4) and b = (2,9,11)
c = a + b
c = (3,7,4) + (2,9,11) = (3+2,7+9,4+11) = (5,16,15)
c = a + b
c = (3,7,4) + (2,9,11) = (3+2,7+9,4+11) = (5,16,15)
Example: subtract (1,2,3,4) from (3,3,3,3)
(3,3,3,3) + −(1,2,3,4)
= (3,3,3,3) + (−1,−2,−3,−4)
= (3−1,3−2,3−3,3−4)
= (2,1,0,−1)
= (3,3,3,3) + (−1,−2,−3,−4)
= (3−1,3−2,3−3,3−4)
= (2,1,0,−1)
Example: what is the magnitude of the vector w = (1,-2,3) ?
|w| = √( 12 + (-2)2 + 32 ) = √( 1+4+9 ) = √14
Magnitude and Direction
You may know a vector's magnitude and direction, but want its x and y lengths (or vice versa):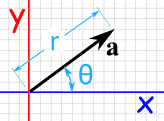 |
<=> | 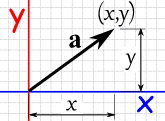 |
| Vector a in Polar Coordinates |
Vector a in Cartesian Coordinates |
| From Polar Coordinates (r,θ) to Cartesian Coordinates (x,y) |
From Cartesian Coordinates (x,y) to Polar Coordinates (r,θ) |
|
|
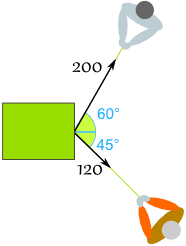 |
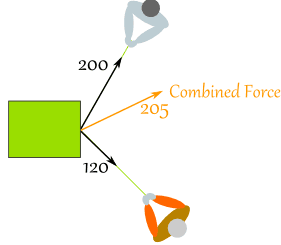
An ExampleSam and Alex are pulling a box.
|
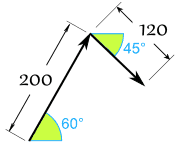
Sam's Vector:
- x = r × cos( θ ) = 200 × cos(60°) = 200 × 0.5 = 100
- y = r × sin( θ ) = 200 × sin(60°) = 200 × 0.8660 = 173.21
- x = r × cos( θ ) = 120 × cos(-45°) = 120 × 0.7071 = 84.85
- y = r × sin( θ ) = 120 × sin(-45°) = 120 × -0.7071 = −84.85
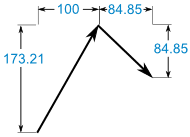
(100, 173.21) + (84.85, −84.85) = (184.85, 88.36)
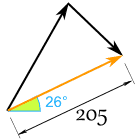
We can convert that to polar for a final answer:- r = √ ( x2 + y2 ) = √ ( 184.852 + 88.362 ) = 204.88
- θ = tan-1 ( y / x ) = tan-1 ( 88.36 / 184.85 ) = 25.5°
| And we have this (rounded) result: | And it looks like this for Sam and Alex: | |
 |
 |
No comments:
Post a Comment