PROBLEM NUMBER 1
A farmer can plant up to 8 acres of land with
wheat and barley. He can earn $5,000 for every
acre he plants with wheat and $3,000 for every
acre he plants with barley. His use of a
necessary pesticide is limited by federal
regulations to 10 gallons for his entire 8 acres.
Wheat requires 2 gallons of pesticide for every
acre planted and barley requires just 1 gallon
per acre.
What is the maximum profit he can make?
SOLUTION TO PROBLEM NUMBER 1
let x = the number of acres of wheat
let y = the number of acres of barley.
since the farmer earns $5,000 for each acre of wheat and $3,000 for each
acre of barley, then the total profit the farmer can earn is 5000*x +
3000*y.
let p = total profit that can be earned. your equation for profit becomes:
p = 5000x + 3000y
that's your objective function. it's what you want to maximize
the constraints are:
number of acres has to be greater than or equal to 0.
number of acres has to be less than or equal to 8.
amount of pesticide has to be less than or equal to 10.
your constraint equations are:
x >= 0
y >= 0
x + y <= 8
2x + y <= 10
to graph these equations, solve for y in those equations that have y in
them and then graph the equality portion of those equations.
x >= 0
y >= 0
y <= 8-x
y <= 10 - 2x
x = 0 is a vertical line that is the same line as the y-axis.
y = 0 is a horizontal line that is the same line as the x-axis.
the area of the graph that satisfies all the constraints is the region of feasibility.
the maximum or minimum solutions to the problem will be at the
intersection points of the lines that bound the region of feasibility.
the graph of your equations looks like this:
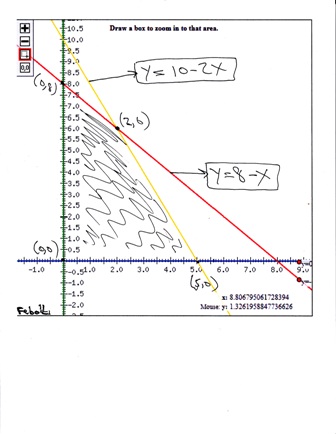
the region of feasibility is the shaded area of the graph.
you can see from this graph that the region of feasibility is bounded by the following (x,y) coordinate points:
(0,0)
(0,8)
(2,6)
(5,0)
the point (0,0) is the intersection of the line x-axis with the y-axis.
the point (0,8) is the intersection of the line y = 8 - x with the y-axis.
the point (5,0) is the intersection of the line y = 10 - 2x with the x-axis.
the point (2,6) is the intersection of the line y = 8 - x with the line y = 10 - 2x.
the point (2,6) was solved for in the following manner:
equations of the intersecting lines are:
y = 8 - x
y = 10 - 2x
subtract the first equation from the second equation and you get:
0 = 2 - x
add x to both sides of this equation and you get:
x = 2
substitute 2 for x in either equation to get y = 6.
that makes the intersection point (x,y) = (2,6).
the objective equation is:
p = 5000x + 3000y
profit will be maximum at the intersection points of the region of feasibility on the graph.
the profit equation is evaluated at each of these points as shown in the following table.
intersection point of (x,y) p
(0,0) $0
(0,8) $24,000
(2,6) $28,000 *****
(5,0) $25,000
the maximum profit occurs when the farmer plants 2 acres of wheat and 6 acres of barley.
number of acres of wheat is 2 and number of acres of barley is 6 for a
total of 8 acres which is the maximum number of acres available for
planting.
number of gallons of pesticide used for wheat is 4 and number of gallons
of pesticide used for barley is 6 for a total of 10 gallons of
pesticide which is the maximum amount of pesticide that can be used.
PROBLEM NUMBER 2
A painter has exactly 32 units of yellow dye and 54 units of green dye.
He plans to mix as many gallons as possible of color A and color B.
Each gallon of color A requires 4 units of yellow dye and 1 unit of green dye.
Each gallon of color B requires 1 unit of yellow dye and 6 units of green dye.
Find the maximum number of gallons he can mix.
SOLUTION TO PROBLEM NUMBER 2
the objective function is to determine the maximum number of gallons he can mix.
the colors involved are color A and color B.
let x = the number of gallons of color A.
let y = the number of gallons of color B.
if we let g = the maximum gallons the painter can make, then the objective function becomes:
g = x + y
make a table for color A and color B to determine the amount of each dye required.
your table will look like this:
each gallon of color A or B will require:
units of yellow dye units of green dye
color A 4 1
color B 1 6
total units of yellow dye available are 32
total units of green dye available are 54
your constraint equations are:
x >= 0
y >= 0
4x + y <= 32
x + 6y <= 54
x and y have to each be greater than or equal to 0 because the number of gallons can't be negative.
in order to graph these equations, you solve for y in those equations that have y in them.
the equtions for graphing are:
x >= 0
y >= 0
y <= 32 - 4x
y <= (54 - x)/6
x = 0 is a vertical line that is the same line as the y-axis.
y = 0 is a horizontal line that is the same line as the x-axis.
the graph will look like this:
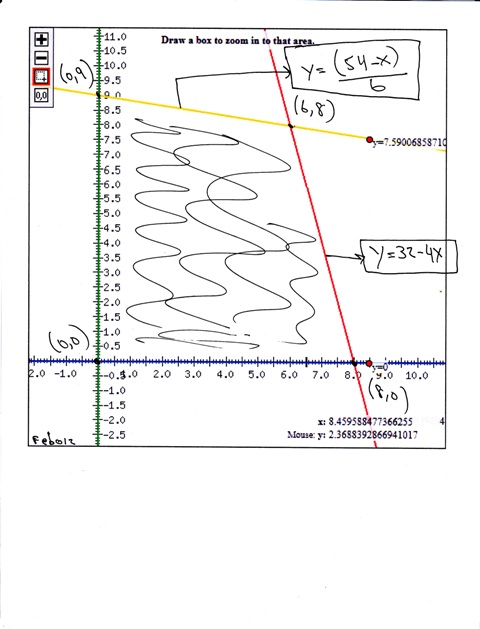
the region of feasibility is the shaded area of the graph.
all points within the feasibility region meet the constraint of the problem.
the intersection points of the region of feasibility are:
(0,0)
(0,9)
(6,8)
(8,0)
the maximum or minimum value of the objective function will be at these points of intersection.
solve the objective function at each of these intersection points to
determine which point contains the maximum number of gallons.
the objective function is:
g = x + y
the table with the value of g at each of these intersection points is shown below:
intersection point (x,y) gallons of paint
(0,0) 0
(0,9) 9
(6,8) 14 *****
(8,0) 8
the maximum gallons of paint for color A and B, given the constraints, is equal to 14.
this is comprised of 6 gallons of color A and 8 gallons of color B.
6 gallons of color A uses 24 gallons of yellow dye and 8 gallons of
color B uses 8 gallons of yellow dye for a total of 32 gallons of yellow
dye which is the maximum amount of yellow dye that can be used.
6 gallons of color A user 6 gallons of green dye and 8 gallons of color B
uses 48 gallons of green dye for a total of 54 gallons of green dye
which is the maximum amount of green dye that can be used.
PROBLEM NUMBER 3
The Bead Store sells material for customers to make their own jewelry.
Customer can select beads from various bins. Grace wants to design her
own Halloween necklace from orange and black beads. She wants to make a
necklace that is at least 12 inches long, but no more than 24 inches
long. Grace also wants her necklace to contain black beads that are at
least twice the length of orange beads. Finally, she wants her necklace
to have at least 5 inches of black beads.
Find the constraints, sketch the problem and find the vertices (intersection points)
SOLUTION TO PROBLEM NUMBER 3
let x = the number of inches of black beads.
let y = the number of inches of orange beads.
the objective function is the length of the necklace
there is a maximum length and a minimum length.
if you let n equal the length of the necklace, then the objective function becomes:
n = x + y
since the problem is looking for the number of inches of black beads and the number of inches of orange beads, we will let:
the constraint equations for this problem are:
x >= 0
y >= 0
x + y >= 12
x + y <= 24
x >= 2y
x >= 5
x >= 0 is there because the number of inches of black beads can't be negative.
y >= 0 is there because the number of inches of orange beads can't be negative.
x + y >= 12 is there because the total length of the necklace has to be greater than or equal to 12 inches.
x + y <= 24 is there because the total length of the necklace has to be less than or equal to 24 inches.
x >= 2y is there because the length of the black beads has to be
greater than or equal to twice the length of the orange beads.
x >= 5 is there because the number of inches of black beads has to be greater than or equal to 5.
to graph these equations, we have to solve for y in each equation that
has y in it and then graph the equality portion of each of them.
your equations for graphing are:
x >= 0
y >= 0
y >= 12 - x
y <= 24 - x
y <= x/2
x >= 5
x = 0 is a vertical line that is the same line as the y-axis.
y = 0 is a horizontal line that is the same line as the x-axis.
x = 5 is a vertical line at x = 5.
a graph of you equations is shown below:
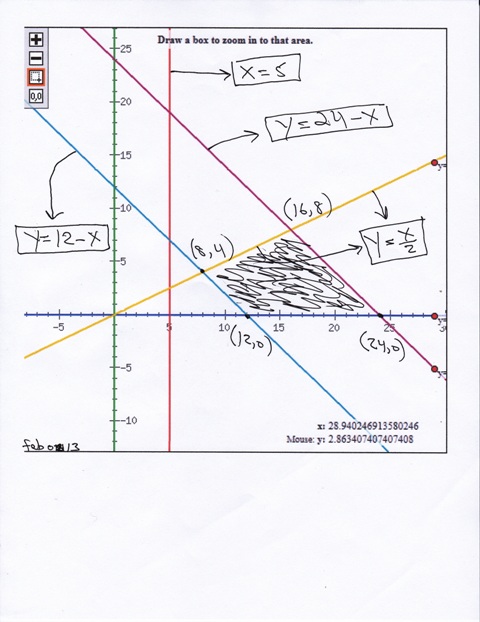
the region of feasibility is the shaded area of the graph.
all points within the region of feasibility meet the constraint requirements of the problem.
the intersection points bounding the region of feasibility are:
(8,4)
(12,0)
(16,8)
(24,0)
(8,4) is the intersection of the lines y = x/2 and y = 12 - x
to find the point of intersection, set x/2 and 12-x equal to each other and solve for xx.
you get:
x/2 = 12-x
multiply both sides of the equation by 2 to get:
x = 24-2x
add 2x to both sides of the equation to get:
3x = 24
divide both sides of the equation by 3 to get:
x = 8.
substitute 8 for x in either equation to get y = 4.
(12,0) is the intersection of the line y = 12 - x with the x-axis.
(24,0) is the intersection of the line y = 24 - x with the x-axis.
to find the point of intersection, set y equal to 0 in each equation and solve for x.
(16,8) is the intersection of the lines y = x/2 and y = 24 - x.
to find the intersection point, set x/2 equal to 24-x and solve for x.
you get:
x/2 = 24-x
multiply both sides of this equation by 2 to get:
x = 48 - 2x
add 2x to both sides of this equation to get:
3x = 48
divide both sides of this equation by 3 to get:
x = 16
substitute 16 for x in either equation to get:
y = 8.
the maximum / minimum necklace length will be at the intersection points of the boundaries of the region of feasibility.
evaluation of the objective function at these intersections yields the following:
objective function is:
x + y = n where n is the length of the necklace in inches.
intersection points number of inches
(8,4) 12
(12,0) 12
(16,8) 24
(24,0) 24
the number of inches of black beads is at least twice the number of inches of orange beads.
the number of inches of black beads is at least 5.
the total length of the necklace is greater than or equal to 12 inches or less than or equal to 24 inches.
all the constraints have been met.
the maximum length the necklace can be and still meet the constraints is 24 inches.
the minimum length the necklace can be and still meet the constraints is 12 inches.
PROBLEM NUMBER 4
A garden shop wishes to prepare a supply of special fertilizer at a minimal cost by mixing two fertilizers, A and B.
The mixture is to contain:
at least 45 units of phosphate
at least 36 units of nitrate
at least 40 units of ammonium
Fertilizer A costs the shop $.97 per pound.
Fertilizer B costs the shop $1.89 per pound.
fertilizer A contains 5 units of phosphate and 2 units of nitrate and 2 units of ammonium.
fertilizer B contains 3 units of phosphate and 3 units of nitrate and 5 units of ammonium.
how many pounds of each fertilizer should the shop use in order to minimize their cost.
SOLUTION TO PROBLEM NUMBER 4
let x = the number of pounds of fertilizer A.
let y = the number of pounds of fertilizer B.
the objective function is to minimize the cost.
the objective function becomes:
c = .97x + 1.89y
the constraint equations are:
since the number of pounds of each fertilizer can't be negative, 2 of the constraint equations become:
x >= 0
y >= 0
since the number of units of phosphate has to be at least 45, the constraint equation for phosphate becomes:
5x + 3y >= 45
since the number of units of nitrate must be at least 36, the constraint equation for nitrates becomes:
2x + 3y >= 36
since the number of units of ammonium must be at least 40, the constraint equation for ammonium becomes:
2x + 5y >= 40
the constraint equations for this problem become:
x >= 0
y >= 0
5x + 3y >= 45
2x + 3y >= 36
2x + 5y >= 40
in order to graph these equations, you have to solve for y in each
equation that has y in it and then graph the equality portion of those
equations.
the equations to be graphed are:
x >= 0
y >= 0
y >= (45-5x)/3
y >= (36 - 2x)/3
y >= (40-2x)/5
x = 0 is a vertical line that is the same line as the y-axis.
y = 0 is a horizontal line that i the same line as the x-axis.
a graph of your equation is shown below:
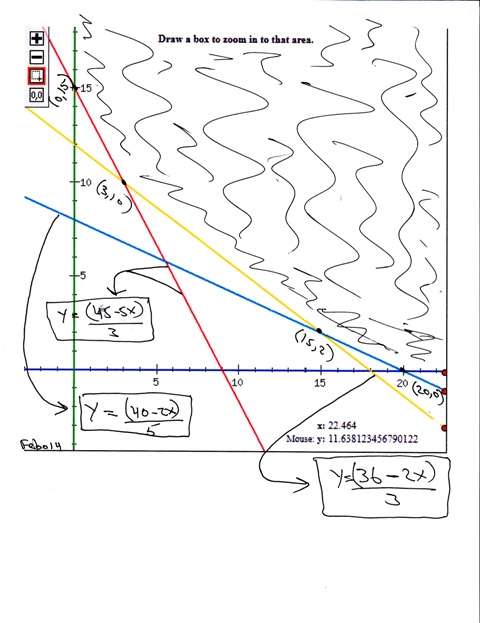
the feasibility region is the area of the graph that is shaded.
all points within the region of feasibility meet the constraint requirements of the problem.
the intersection points at the boundaries of the feasibility region are:
(0,15)
(3,10)
(15,2)
(20,0)
the intersection points of the boundaries of the region of feasibility
contain the minimum cost solution for the objective function in this
problem.
now that you have the intersection points, you can solve for the minimum cost equation which is the objective function of:
c = .97x + 1.89y
the following table shows the value of the cost equation at each of the intersection points.
intersection points (x,y) c = .97x + 1.89y minimum solution
(0,15) 28.35
(3,10) 21.81
(15,2) 18.33 *****
(20,0) 19.40
the table suggests that we have a minimum cost solution when the value of x is equal to 15 and the value of y is equal 2.
when x = 15 and y = 2, the number of pounds of potassium, nitrates, and ammonium are:
phosphate = 5x + 3y = 5*15 + 3*2 = 75 + 6 = 81
nitrate = 2x + 3y = 2*15 + 3*2 = 30 + 6 = 36
ammonium = 2x + 5y = 2*15 + 5*2 = 30 + 10 = 40
all the constraints associated with the minimum cost objective have been met.
No comments:
Post a Comment