Saturday, April 19, 2014

LINEAR PROGRAMMING----- FORM FOUR.

LINEAR    PROGRAMMING-----FORM  FOUR

Sections: Optimizing linear systems, Setting up word problems
INTRODUCTION:

Linear programming is the process of taking various linear inequalities relating to some situation, and finding the "best" value obtainable under those conditions. A typical example would be taking the limitations of materials and labor, and then determining the "best" production levels for maximal profits under those conditions.
In "real life", linear programming is part of a very important area of mathematics called "optimization techniques". This field of study (or at least the applied results of it) are used every day in the organization and allocation of resources. These "real life" systems can have dozens or hundreds of variables, or more. In algebra, though, you'll only work with the simple (and graphable) two-variable linear case.
The general process for solving linear-programming exercises is to graph the inequalities (called the "constraints") to form a walled-off area on the x,y-plane (called the "feasibility region"). Then you figure out the coordinates of the corners of this feasibility region (that is, you find the intersection points of the various pairs of lines), and test these corner points in the formula (called the "optimization equation") for which you're trying to find the highest or lowest value.



  • Find the maximal and minimal value of z = 3x + 4y subject to the following constraints:
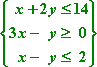
      • x + 2y <= 14, 3x - y >= 0, x - y <= 2
    The three inequalities in the curly braces are the constraints. The area of the plane that they mark off will be the feasibility region. The formula "z = 3x + 4y" is the optimization equation. I need to find the (x, y) corner points of the feasibility region that return the largest and smallest values of z.
    My first step is to solve each inequality for the more-easily graphed equivalent forms:
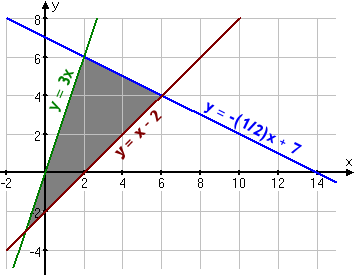
      y <= -(1/2)x + 7, y <= 3x, y >= x - 2
    It's easy to graph the system:   Copyright © Elizabeth Stapel 2006-2011 All Rights Reserved
      graph of inequalities, with lines labelled and feasibility region shaded in
    To find the corner points -- which aren't always clear from the graph -- I'll pair the lines (thus forming a system of linear equations) and solve:
      y = –( 1/2 )x + 7y = 3x
      y = –( 1/2 )x + 7y = x – 2
      y = 3x
      y       = x – 2
      –( 1/2 )x + 7 = 3x–x + 14 = 6x14 = 7x
      2 =       x
      y = 3(2) = 6
      –( 1/2 )x + 7 = x – 2
      –      x + 14 = 2x – 4
      18 = 3      x
      6 =       x
      y = (6) – 2 = 4
      3x = x – 2
      2      x = –2x = –1
      y = 3(–1) = –3
      corner point at (2, 6)
      corner point at (6, 4)
      corner pt. at (–1, –3)
    So the corner points are (2, 6), (6, 4), and (–1, –3).
    Somebody really smart proved that, for linear systems like this, the maximum and minimum values of the optimization equation will always be on the corners of the feasibility region. So, to find the solution to this exercise, I only need to plug these three points into "z = 3x + 4y".
      (2, 6):      z = 3(2)   + 4(6)   =   6 + 24 =   30
      (6, 4):            z = 3(6)   + 4(4)   = 18 + 16 =   34
      (–1, –3):  z = 3(–1) + 4(–3) = –3 – 12 = –15
    Then the maximum of z = 34 occurs at (6, 4),
    and     the minimum of z = –15 occurs at (–1, –3).
    • Given the following constraints, maximize and minimize the value of z = –0.4x + 3.2y.
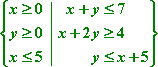
        • x >= 0, y >= 0, x <= 5, x + y <= 7, x + 2y >= 4, y <= x + 5
      First I'll solve the fourth and fifth constraints for easier graphing:
        x >= 0, y >= 0, x <= 5, y <= -x + 7, y >= -(1/2)x + 2, y <= x + 5
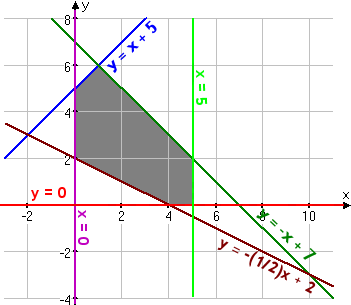
      The feasibility region looks like this:
        feasibility region
      From the graph, I can see which lines cross to form the corners, so I know which lines to pair up in order to verify the coordinates. I'll start at the "top" of the shaded area and work my way clockwise around the edges:
        y = –x + 7y = x + 5
        y = –x + 7x = 5
        x = 5y = 0
        –x + 7 = x + 5
        2 = 2        x
        1 =         x
        y = (1) + 5 = 6
        y = –(5) + 7 = 2
        [nothing to do]
        corner at (1, 6)
        corner at (5, 2)
        corner at (5, 0)

        y = 0y = –( 1/2 )x + 2
        y = –( 1/2 )x + 2x = 0
        x = 0y = x + 5
        –( 1/2 )x + 2 = 0
        2 = (1/2)x
        4 = x
        y = –( 1/2 )(0) + 2
        y = 0 + 2
        y = 2
        y = (0) + 5 = 5
        corner at (4, 0)
        corner at (0, 2)
        corner at (0, 5)
      Now I'll plug each corner point into the optimization equation, z = –0.4x + 3.2y:
        (1, 6):  z = –0.4(1) + 3.2(6) = –0.4 + 19.2 = 18.8
        (5, 2):  z = –0.4(5) + 3.2(2) = –2.0 + 6.4   =   4.4
        (5, 0):  z = –0.4(5) + 3.2(0) = –2.0 + 0.0   = –2.0
        (4, 0):  z = –0.4(4) + 3.2(0) = –1.6 + 0.0   = –1.6
        (0, 2):  z = –0.4(0) + 3.2(2) = –0.0 + 6.4   =   6.4
        (0, 5):  z = –0.4(0) + 3.2(5) = –0.0 + 16.0 = 16.0
      Then the maximum is 18.8 at (1, 6) and the minimum is –2 at (5, 0).
Given the inequalities, linear-programming exercise are pretty straightforward, if sometimes a bit long. The hard part is usually the word problems, where you have to figure out what the inequalities are. So I'll show how to set up some typical linear-programming word problems.
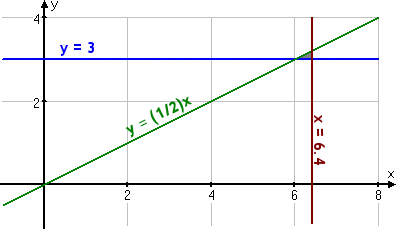
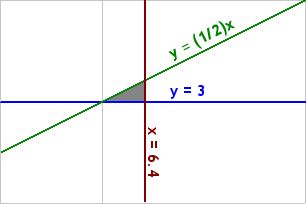
  • At a certain refinery, the refining process requires the production of at least two gallons of gasoline for each gallon of fuel oil. To meet the anticipated demands of winter, at least three million gallons of fuel oil a day will need to be produced. The demand for gasoline, on the other hand, is not more than 6.4 million gallons a day.
    • If gasoline is selling for $1.90 per gallon and fuel oil sells for $1.50/gal, how much of each should be produced in order to maximize revenue?
    The question asks for the number of gallons which should be produced, so I should let my variables stand for "gallons produced".
    ADVERTISEMENT


      x: gallons of gasoline producedy: gallons of fuel oil produced
    Since this is a "real world" problem, I know that I can't have negative production levels, so the variables can't be negative. This gives me my first two constraints: namely, x > 0 and y > 0.
    Since I have to have at least two gallons of gas for every gallon of oil, then x > 2y.
    For graphing, of course, I'll use the more manageable form "y < ( 1/2 )x".
    The winter demand says that y > 3,000,000; note that this constraint eliminates the need for the "y > 0" constraint. The gas demand says that x < 6,400,000.

    I need to maximize revenue R, so the optimization equation is R = 1.9x + 1.5y. Then the model for this word problem is as follows:
      R = 1.9x + 1.5y, subject to:
      x       > 0
      x < 6,400,000         Copyright © Elizabeth Stapel 2006-2011 All Rights Reserved
      y > 3,000,000
      y < ( 1/2 )x
    Using a scale that counts by millions (so "y = 3" on the graph means "y is three million"), the above system graphs as follows:
      feasibility region
    Taking a closer look, I can see the feasibility region a little better:
      close-up of feasibility region
When you test the corner points at (6.4m, 3.2m), (6.4m, 3m), and (6m, 3m), you should get a maximal solution of R = $16.96m at (x, y) = (6.4m, 3.2m).
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)