LINEAR PROGRAMMING: WORD PROBLEMS ----FORM FOUR BY. MWL. JAPHET MASATU.

LINEAR   PROGRAMMING: WORD   PROBLEMS.

---

INTRODUCTION:

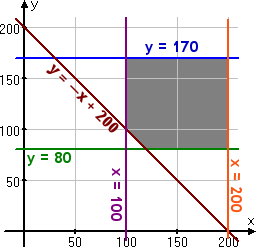
• A calculator company produces a scientific calculator and a graphing calculator. Long-term projections indicate an expected demand of at least 100 scientific and 80 graphing calculators each day. Because of limitations on production capacity, no more than 200 scientific and 170 graphing calculators can be made daily. To satisfy a shipping contract, a total of at least 200 calculators much be shipped each day.
If each scientific calculator sold results in a $2 loss, but each graphing calculator produces a $5 profit, how many of each type should be made daily to maximize net profits?
The question asks for the optimal number of calculators, so my variables will stand for that:

x: number of scientific calculators producedy: number of graphing calculators produced
Since they can't produce negative numbers of calculators, I have the two constraints, x > 0 and y > 0. But in this case, I can ignore these constraints, because I already have that x > 100 and y > 80. The exercise also gives maximums: x < 200 and y < 170. The minimum shipping requirement gives me x + y > 200; in other words, y > –x + 200. The revenue relation will be my optimization equation: R = –2x + 5y. So the entire system is:

R = –2x + 5y, subject to:
100 < x < 200 
80 <  y < 170 
y > –x + 200 

The feasibility region graphs as:   Copyright © Elizabeth Stapel 2006-2011 All Rights Reserved

When you test the corner points at (100, 170), (200, 170), (200, 80), (120, 80), and (100, 100), you should obtain the maximum value of R = 650 at (x, y) = (100, 170). That is, the solution is "100 scientific calculators and 170 graphing calculators".

---

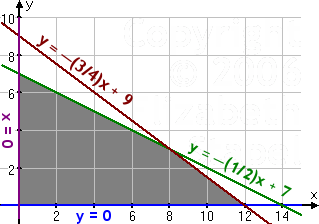
• You need to buy some filing cabinets. You know that Cabinet X costs $10 per unit, requires six square feet of floor space, and holds eight cubic feet of files. Cabinet Y costs $20 per unit, requires eight square feet of floor space, and holds twelve cubic feet of files. You have been given $140 for this purchase, though you don't have to spend that much. The office has room for no more than 72 square feet of cabinets. How many of which model should you buy, in order to maximize storage volume?
The question ask for the number of cabinets I need to buy, so my variables will stand for that:

x: number of model X cabinets purchasedy: number of model Y cabinets purchased
Naturally, x > 0 and y > 0. I have to consider costs and floor space (the "footprint" of each unit), while maximizing the storage volume, so costs and floor space will be my constraints, while volume will be my optimization equation.

cost: 10x + 20y < 140, or y < –( ¹/₂ )x + 7
space: 6x + 8y < 72, or y < –( ³/₄ )x + 9
volume: V = 8x + 12y
This system (along with the first two constraints) graphs as:

When you test the corner points at (8, 3), (0, 7), and (12, 0), you should obtain a maximal volume of 100 cubic feet by buying eight of model X and three of model Y .               Linear Programming: More Word Problems Sections: Optimizing linear systems, Setting up word problems

---

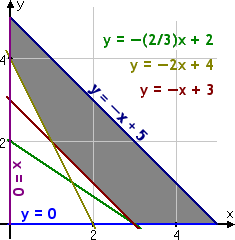
• In order to ensure optimal health (and thus accurate test results), a lab technician needs to feed the rabbits a daily diet containing a minimum of 24 grams (g) of fat, 36 g of carbohydrates, and 4 g of protien. But the rabbits should be fed no more than five ounces of food a day.
Rather than order rabbit food that is custom-blended, it is cheaper to order Food X and Food Y, and blend them for an optimal mix. Food X contains 8 g of fat, 12 g of carbohydrates, and 2 g of protein per ounce, and costs $0.20 per ounce. Food Y contains 12 g of fat, 12 g of carbohydrates, and 1 g of protein per ounce, at a cost of $0.30 per ounce.
What is the optimal blend?
Since the exercise is asking for the number of ounces of each food required for the optimal daily blend, my variables will stand for the number of ounces of each:

x: number of ounces of Food Xy: number of ounces of Food Y
Since I can't use negative amounts of either food, the first two constrains are the usual ones: x > 0 and y > 0. The other constraints come from the grams of fat, carbohydrates, and protein per ounce:

fat:        8x + 12y > 24
carbs:  12x + 12y > 36
protein:  2x +   1y >   4
Also, the maximum weight of the food is five ounces, so:


x + y < 5
The optimization equation will be the cost relation C = 0.2x + 0.3y, but this time I'll be finding the minimum value, not the maximum.
After rearranging the inequalities, the system graphs as:

(Note: One of the lines above is irrelevant to the system. Can you tell which one?)

When you test the corners at (0, 4), (0, 5), (3, 0), (5, 0), and (1, 2), you should get a minimum cost of sixty cents per daily serving, using three ounces of Food X only.

---

Sometimes you'll have more than just two things to deal with. The next example has three things to juggle; the next page provides an example of juggling four things.

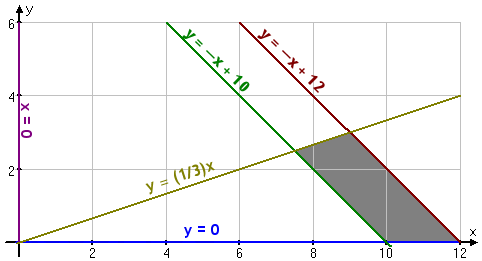
• You have $12,000 to invest, and three different funds from which to choose. The municipal bond fund has a 7% return, the local bank's CDs have an 8% return, and the high-risk account has an expected (hoped-for) 12% return. To minimize risk, you decide not to invest any more than $2,000 in the high-risk account. For tax reasons, you need to invest at least three times as much in the municipal bonds as in the bank CDs. Assuming the year-end yields are as expected, what are the optimal investment amounts?
Since the question is asking me to find the amount of money for each account, my variables will need to stand for those amounts. Since I'd like to deal with smaller numbers, I'll count by thousands, so:

x: amount (in thousands) invested in bondsy: amount (in thousands) invested in CDs
Um... now what? I only have two variables, but I have three accounts. To handle this, I need the "how much is left" construction:

12 – x – y: amount (in thousands) invested in the high-risk account
I can't invest negative amounts of money, so the first two constraints are the usual ones: x > 0 and y > 0. The amount in the high-risk account can't be negative either, so 12 – x – y > 0, which simplifies as:

y < –x + 12
Also, the upper limit on the high-risk account gives me the inequality (12 – x – y) < 2. This simplifies as:   Copyright © Elizabeth Stapel 2006-2011 All Rights Reserved

y > –x + 10
And the tax requirements give me y < ( ¹/₃ )x. The optimization equation will be the total investment yield, Y = 0.07x + 0.08y + 0.12(12 – x – y) = 1.44 – 0.05x – 0.04y. The entire system is then as follows:

Maximize Y = 1.44 – 0.05x – 0.04y, subject to:
  x > 0
  y > 0
  y > –x + 10
  y < –x + 12
  y < ( ¹/₃ )x
The feasibility region graphs as:

When you test the corner points at (9, 3), (12, 0), (10, 0), and (7.5, 2.5), you should get an optimal return of $965 when you invest $7,500 in municipal bonds, $2,500 in CDs, and the remaining $2,000 in the high-risk account.